Web supplementary information for "Reverse engineering molecular regulatory networks from microarray data with qp-graphs" by R. Castelo and A. Roverato, J Comp Biol, 16(2):213-227, 2009
In this web supplementary information we provide data files and R scripts to help reproducing some of the results contained in our paper "Reverse engineering molecular regulatory networks from microarray data with qp-graphs".Estimation of average non-rejection rates and comparison with other methods
The estimation of average non-rejection rates was carried out using the parallel standalone version of the qp package software available at this link. This program reads directly the sample covariance matrix of the data and thus we provide here links to the compressed flat files containing the two sample covariance matrices, calculated using the cov function in R, employed in this calculation:| M3d data: | m3dv4b5.scovmat.txt.gz (17 M) |
| Oxygen deprivation data: | GDS680.scovmat.txt.gz (145 M) |
Using these sample covariance matrices, non-rejection rates were estimated for a wide range of q-order values for each corresponding matrix. The collection of files containing these estimates are included in the following tar balls:
| M3d data: | NRRsM3dV4B5.tar.gz (51 M) |
| Oxygen deprivation data: | NRRsGDS680.tar.gz (242 M) |
In what follows, we show how to manipulate these data on R only for the Oxygen deprivation data set. The M3d data can be treated analogously. We will need Bioconductor with the current development version 2.4.0 and thus also the current pre-release version of R (>= 2.9.0) running and available from the CRAN repository for download. We start by loading the corresponding packages and calculating an average non-rejection rate (as the arithmetic mean) from the estimated non-rejection rates. We assume the tar ball NRRsGDS680.tar.gz has been uncompressed in the same directory where we are running the R session:
library(Biobase)
library(annotate)
library(tools)
library(GOstats)
library(org.EcK12.eg.db)
library(qpgraph)
data(EcoliOxygen)
p <- dim(gds680.eset)["Features"]
avgnrr.estimates <- matrix(as.double(0), nrow=p, ncol=p)
nrrfiles <- list.files("NRRsGDS680", full.names=TRUE)
for (filename in nrrfiles) {
# we know before hand that we used nTests=100
nrr.estimates <- qpImportNrr(filename, nTests=100)
avgnrr.estimates <- avgnrr.estimates +
(1 / length(nrrfiles)) * nrr.estimates
}
rownames(avgnrr.estimates) <- featureNames(gds680.eset)
colnames(avgnrr.estimates) <- featureNames(gds680.eset)
next, we also use Pearson correlation coefficients as a reverse-engineering method:
pcc.estimates <- qpPCC(gds680.eset)and finally, we use the assignment of random correlations as a baseline comparison doing the following:
rndcor <- matrix(runif(p*p, min=-1, max=+1), nrow=p, ncol=p) rownames(rndcor) <- colnames(rndcor) <- featureNames(gds680.eset)We will compare the performance of these three methods by calculating precision-recall curves and for this purpose we need an incidence matrix of the RegulonDB interactions and separate vectors with the transcription factor and target gene names involved in the RegulonDB transcriptional network with respect to which the precision-recall curve is calculated:
allOrderedGenes <- featureNames(gds680.eset)
regulonTFgenes <- as.character(unique(filtered.regulon6.1[, "EgID_TF"]))
regulonTGgenes <- as.character(unique(c(regulonTFgenes,
filtered.regulon6.1[, "EgID_TG"])))
filtered.regulon6.1.I <- matrix(FALSE, nrow=p, ncol=p)
rownames(filtered.regulon6.1.I) <- allOrderedGenes
colnames(filtered.regulon6.1.I) <- allOrderedGenes
TFi <- match(filtered.regulon6.1[, "EgID_TF"], allOrderedGenes)
TGi <- match(filtered.regulon6.1[, "EgID_TG"], allOrderedGenes)
filtered.regulon6.1.I[cbind(TFi,TGi)] <- TRUE
filtered.regulon6.1.I[cbind(TGi,TFi)] <- TRUE
We can now calculate the three precision-recall curves as follows:
avgnrr.pr <- qpPrecisionRecall(avgnrr.estimates,
filtered.regulon6.1.I, decreasing=FALSE,
pairup.i=regulonTFgenes,
pairup.j=regulonTGgenes,
recallSteps=c(seq(0,0.1,0.005),
seq(0.1,1.0,0.1)))
abspcc.pr <- qpPrecisionRecall(abs(pcc.estimates$R),
filtered.regulon6.1.I, decreasing=TRUE,
pairup.i=regulonTFgenes,
pairup.j=regulonTGgenes,
recallSteps=c(seq(0,0.1,0.005),
seq(0.1,1.0,0.1)))
absrnd.pr <- qpPrecisionRecall(abs(rndcor),
filtered.regulon6.1.I, decreasing=TRUE,
pairup.i=regulonTFgenes,
pairup.j=regulonTGgenes,
recallSteps=c(seq(0,0.1,0.005),
seq(0.1,1.0,0.1)))
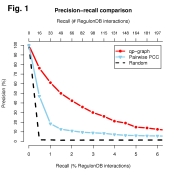
and plot the resulting curves using the code below which produces
the Figure 1 which we may see on the right:
par(mai=c(0.5, 0.5, 1.0, 0.5), mar=c(5, 4, 7, 2) + 0.1)
plot(absrnd.pr[,c(1,2)], type="l", lty=2, lwd=4,
col="black", xlim=c(0,0.06), ylim=c(0,1), axes=FALSE,
xlab="Recall (% RegulonDB interactions)",
ylab="Precision (%)")
axis(1, at=seq(0,1,0.01), labels=seq(0,100,1))
axis(2, at=seq(0,1,0.10), labels=seq(0,100,10),
cex.axis=0.85)
axis(3, at=avgnrr.pr[,"Recall"],
labels=round(avgnrr.pr[,"Recall"] *
dim(filtered.regulon6.1)[1], digits=0),
cex.axis=0.85)
title(main="Precision-recall comparison", line=+5)
lines(avgnrr.pr[,c(1,2)], type="b", lty=1, pch=19,
cex=0.65, lwd=4, col="red")
lines(abspcc.pr[,c(1,2)], type="b", lty=1, pch=25,
cex=0.65, lwd=4, col="skyblue")
mtext("Recall (# RegulonDB interactions)", 3, line=+3)
legend(0.04, 1.0, c("qp-graph","Pairwise PCC", "Random"),
col=c("red", "skyblue", "black"), lty=c(1, 1, 2),
pch=c(19, 25, -1), lwd=3, bg="white", pt.cex=0.85)
mtext("Fig. 1", font=2, line=5, at=-0.005, cex=1.7)
Estimation of functional coherence of the reverse-engineered networks
From the previous calculations one can reverse-engineer networks at particular nominal levels of precision and recall, or with a fixed size on the number of interactions. On any of these networks we can assess their functional coherence (FC) using the qpgraph package and we illustrate here such calculation for a 50%-precision network obtained from the estimated average non-rejection rates previously stored in avgnrr.estimates:Using the previously calculated precision-recall functions, estimate the thresholds that output a 50%-precision network for each method (see help(qpPRscoreThreshold) for an explanation on the parameter usage):
avgnrr.thr <- qpPRscoreThreshold(avgnrr.pr, level=0.50,
recall.level=FALSE, max.score=0)
abspcc.thr <- qpPRscoreThreshold(abspcc.pr, level=0.50,
recall.level=FALSE, max.score=1)
absrnd.thr <- qpPRscoreThreshold(absrnd.pr, level=0.50,
recall.level=FALSE, max.score=1)
Build the network at 50%-precision level using the previously estimated
threshold (see help(qpGraph) and help(qpAnyGraph) for an
explanation on the parameter usage):
qpg50pre <- qpGraph(avgnrr.estimates, avgnrr.thr,
pairup.i=regulonTFgenes,
pairup.j=allOrderedGenes)
pcc50pre <- qpAnyGraph(abs(pcc.estimates$R), abspcc.thr,
remove="below", pairup.i=regulonTFgenes,
pairup.j=allOrderedGenes)
rnd50pre <- qpAnyGraph(abs(rndcor), absrnd.thr,
remove="below", pairup.i=regulonTFgenes,
pairup.j=allOrderedGenes)
Estimate functional coherence of the obtained networks (see
help(qpFunctionalCoherence) for an explanation on the parameter usage):
qpg50preFC <- qpFunctionalCoherence(A=qpg50pre,
TFgenes=regulonTFgenes,
chip="org.EcK12.eg.db",
minRMsize=5, verbose=TRUE)
pcc50preFC <- qpFunctionalCoherence(A=pcc50pre,
TFgenes=regulonTFgenes,
chip="org.EcK12.eg.db",
minRMsize=5, verbose=TRUE)
rnd50preFC <- qpFunctionalCoherence(A=rnd50pre,
TFgenes=regulonTFgenes,
chip="org.EcK12.eg.db",
minRMsize=5, verbose=TRUE)
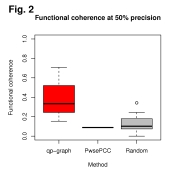
Finally, we can look at the distribution of functional coherence by plotting
the estimated values as follows and which we may see in Figure 2 on the right:
boxplot(qpg50preFC$functionalCoherenceValues,
pcc50preFC$functionalCoherenceValues,
rnd50preFC$functionalCoherenceValues,
names=c("qp-graph", "PwsePCC", "Random"),
col=c("red", "skyblue", "grey"),
main="Functional coherence at 50% precision",
ylim=c(0,1), xlab="Method",
ylab="Functional coherence")
In our JCB article we have assessed FC in this way for the networks obtained
above and also in networks obtained with three other pieces of software: CLR (v1.2),
ARACNE (single-processor no-bootstrap version) and GeneNet (v1.2.1).
We provide here directly the resulting matrices of pairwise measures that these
methods calculate for every pair of genes on the oxygen deprivation data as an
RData file containing the R objects of these matrices:
| Other Methods: | GDS680.clr.aracne.genenet.RData (357 M) |
The entire set of results on functional coherence in the JCB paper can be reproduced by running the the R-script file calculateFC4AllMethods.R in the following way from the R shell running on the directory where the previous files were stored:
source("calculateFC4AllMethods.R")
After about 2.5 hours (depending on your hardware) you will get as a result a file
called FC4AllMethods.RData containing the following R objects:
| regulonFCwithNoise | functional coherence for RegulonDB and different levels of noise. |
| regulonFCwithNoiseCor | Pearson correlation coefficients of the genes introducing noise in RegulonDB with respect to the transcription factor of the module where they were introduced. |
| XXX3rec | incidence matrix of the network at 3% recall for method XXX. |
| XXX3recFC | functional coherence for the network in XXX3rec. |
| XXX50pre | incidence matrix of the network at 50% precision for method XXX. |
| XXX50preFC | functional coherence for the network in XXX50pre. |
| XXX1000sze | incidence matrix of the network with 1000 interactions for method XXX. |
| XXX1000szeFC | functional coherence for the network in XXX1000sze. |
Each of the XXX3recFC, XXX50preFC and XXX1000szeFC objects are R lists with slots txRegNet, txRegNetGO and functionalCoherenceValues where the latter contains the values of functional coherence for each regulatory module where this calculation was done. The other two slots contain intermediate results that allow one to monitor what are the initial set of target genes for each transcription factor and among those, which ones had GO annotations that enable the calculation.
R session information
In order to facilitate running the code and reproducing the previous results here we provide the information about our configuration of R:sessionInfo() R version 2.11.0 (2010-04-22) x86_64-unknown-linux-gnu locale: [1] C attached base packages: [1] tools stats graphics grDevices utils datasets methods [8] base other attached packages: [1] GO.db_2.4.1 qpgraph_1.4.0 org.EcK12.eg.db_2.4.1 [4] GOstats_2.14.0 RSQLite_0.8-4 DBI_0.2-5 [7] graph_1.26.0 Category_2.14.0 annotate_1.26.0 [10] AnnotationDbi_1.10.0 Biobase_2.8.0 loaded via a namespace (and not attached): [1] GSEABase_1.10.0 RBGL_1.24.0 XML_2.8-1 genefilter_1.30.0 [5] splines_2.11.0 survival_2.35-8 xtable_1.5-6